Game Science: GTA V's Stunt Jump System

I'm pretty into Grand Theft Auto V speedrunning. One of my favourite categories is called "StuntJump%", a race starting just after the end of the prologue, and concluding when all fifty of the game's "stunt jumps" have been successfully completed.

As a videogame cheat developer, I started wondering what kind of tools could assist with the StuntJump% speedrun, and landed on the idea of a tool that shows the exact bounds of the landing zones in which a stunt jump completes successfully.¹

But, in order to write a tool, we have to know how the validity check is performed.

Reverse Engineering

Since Grand Theft Auto V is a big game, there's a lot of code in there to reverse. While I did use some reverse engineering tools to get at some of the data used, I couldn't find the bool stunt_jump_landing_valid(Vec3) needle in the haystack that is all of GTA V's executable code.

However, we do get some useful information, courtesy of the engine GTA V uses, the flagship engine from Rockstar Games (the developers of GTA V): The Rockstar Advanced Game Engine. RAGE has a scripting subsystem that lets us get at a lot of game logic information without needing to read through a bunch of heavily-vectorized (and virtualized, I think) assembly listings.

Rockstar Advanced Scripting Engine

Since so many people work on GTA V, it's infeasible for Rockstar to have everybody who needs to write behaviour logic contribute to the game's main code (that's a lot of compiling!). To manage this, the RAGE engine uses a scripting interface, with an embedded bytecode VM that the scripting language targets. This enables the game developers to write logic for missions and other small-scale projects. Scripts are distributed in the game's assets (mostly packed in a proprietary archive format) in the form of the proprietary .ysc program format.

In order for script logic to have any effect on the game itself, RAGE exposes an API to the scripting interface in the form of script natives. Like many script elements, natives are identified by a Jenkins one-at-a-time hash, often abbreviated to joaat in code. Their names are recovered either through leaked side-channel information, guess-and-checking against the hash, or by simply brute-forcing the hash (joaat is trivial to parallelise using GPGPU, and brute-forcing is made even easier by the restricted [A-Z0-9_]+ character set utilised by Rockstar).

The Grand Theft Auto V modding community maintains several databases² of these script natives' names, hashes, and crowdsourced documentation.

NativeDB and Stunt Jumps

Perusing the FiveM native DB, we see a few natives that are involved in stunt jumps (search for stunt_jump):

• MISC::ADD_STUNT_JUMP(startVec1, startVec2, endVec1, endVec2, camVec, ...)
• MISC::ADD_STUNT_JUMP_ANGLED(startVec1, startVec2, startUnk, endVec1, endVec2, endUnk, camVec, ...)
• MISC::ENABLE_STUNT_JUMP_SET(i)

Both ADD_STUNT_JUMP and ADD_STUNT_JUMP_ANGLED also take three unknown int32_t parameters which seem to be always 150, 0, 0, which was abbreviated for, uh, brevity.

ADD_STUNT_JUMP looks simple, jumping from an axis-aligned bounding box defined by the first two vectors, being its two corners in 3D, and landing in a second axis-aligned bounding box that is constructed using the next two vectors. camVec just defines where to place the 'stunt camera' that tracks the car throughout the stunt jump.

Here are the notes for the two unknown floats startUnk and endUnk in the FiveM native database, where they are called radius1 and radius2:

radius1, radius2: Probably a "feather" radius for entry zone, you need to enter the jump within the min/max coordinates, or within this radius of those two coordinates.

We'll come back to this later. First, let's get some information about the jumps themselves:

Decompiled Scripts

I have my own decompiler for RAGE-compiled .ysc script files, but even the use of a search engine can yield decompiled scripts for the latest version of the game.³ When we decompile standard_global_reg.ysc, we find a function that defines all fifty of the game's stunt jumps. You can find a cleaned-up data dump of them here. It looks like:

ADD_STUNT_JUMP_ANGLED(2.143237, 1720.526001, 224.362198, 14.620720, 1712.374023, 230.379395, -6.000000, 98.661507, 1846.069946, 173.665298, 41.456581, 1758.399048, 213.036102, -30.000000, 58.200001, 1729.599976, 228.100006, 150, 0, 0);
ADD_STUNT_JUMP_ANGLED(-437.435699, -1196.306030, 52.999470, -442.850494, -1190.487061, 57.125351, -6.000000, -435.020386, -1242.034058, 48.434071, -448.880402, -1342.776001, 30.265720, -24.000000, -462.662689, -1212.355957, 58.366299, 150, 0, 0);
ADD_STUNT_JUMP_ANGLED(466.720001, 4319.375000, 59.958542, 474.211609, 4328.238770, 64.004349, -8.000000, 401.468109, 4394.319824, 61.782749, 450.532898, 4342.308105, 66.884262, 25.750000, 454.123505, 4323.500977, 68.739319, 150, 0, 0);
// Continue for 47 more jumps...

As a matter of trivia, there are only three non-angled (axis-aligned) stunt jumps in the game:

Anyway, I digress. Now that we have jump data, we can do some science to figure out how ADD_STUNT_JUMP_ANGLED works.

The Scientific Method

Since we can't find the exact logic for the stunt jump calculation, we will have to result to the scientific method. Also known as "trial and error, but you write results down."

Setting Up

Let's do some experiments and conjecture a model to represent the stunt jumps.

Let's inject a mod into GTA V so that we can initiate a jump, and hit a key to cancel the car's velocity and teleport to a certain location to precisely test the stunt jump detection logic.

We set up a Script Hook V mod, and in the main function we can constantly poll the keyboard:

#include "keyboard.h" // Included with the ScriptHookV SDK

void teleport_the_car();

void main() {
  while (true) {
    // When we hit the F13 key, teleport the car
    if (IsKeyDown(VK_F13)) {
      teleport_the_car();
    }

    WAIT(0);
  }
}

Teleporting the car is also easy:

void teleport_the_car() {
  // Quick-and-dirty testing: Change these values and reload the mod.
  float x = 0.f;
  float y = 0.f;
  float z = 1000.f;

  // 'Ped' means 'Pedestrian' - The player as a humanoid entity.
  Ped ped = PLAYER::PLAYER_PED_ID();
  if (Vehicle car = PED::GET_VEHICLE_PED_IS_IN(ped, false)) {
    // Ignore the three falses here, they're labeled as 'invertAxis{X,Y,Z}' in the docs.
    ENTITY::SET_ENTITY_COORDS_NO_OFFSET(car, x, y, z, false, false, false);

    // Set the velocity to be moving slightly downwards,
    // as the game might cancel a stunt jump when your velocity becomes [0, 0, 0].
    ENTITY::SET_ENTITY_VELOCITY(car, 0.f, 0.f, -0.25f);
  }
}

All we have to do is hit F13⁴ after we've started the jump, and we'll get teleported to a spot of our choosing.

In the end, we get a result like this (we're purposefully airstuck while holding the key):

Regular Regions

First, let's verify that non-angled jumps work as we would expect: A regular, good-old is-point-in-AABB check:

struct AxisAlignedRegion {
  struct Vector3 minCorner;
  struct Vector3 maxCorner;
}

function AxisAlignedRegion.contains(point: Vector3) {
  return (point.x >= minCorner.x && point.x <= maxCorner.x) &&
    (point.y >= minCorner.y && point.y <= maxCorner.y) &&
    (point.z >= minCorner.z && point.z <= maxCorner.z);
}

Teleporting straight to the corner of a regular region for the jump from the hospital stairs gives us a success, and moving out by 0.5 units gives us a fail. It looks like everything is working just fine.

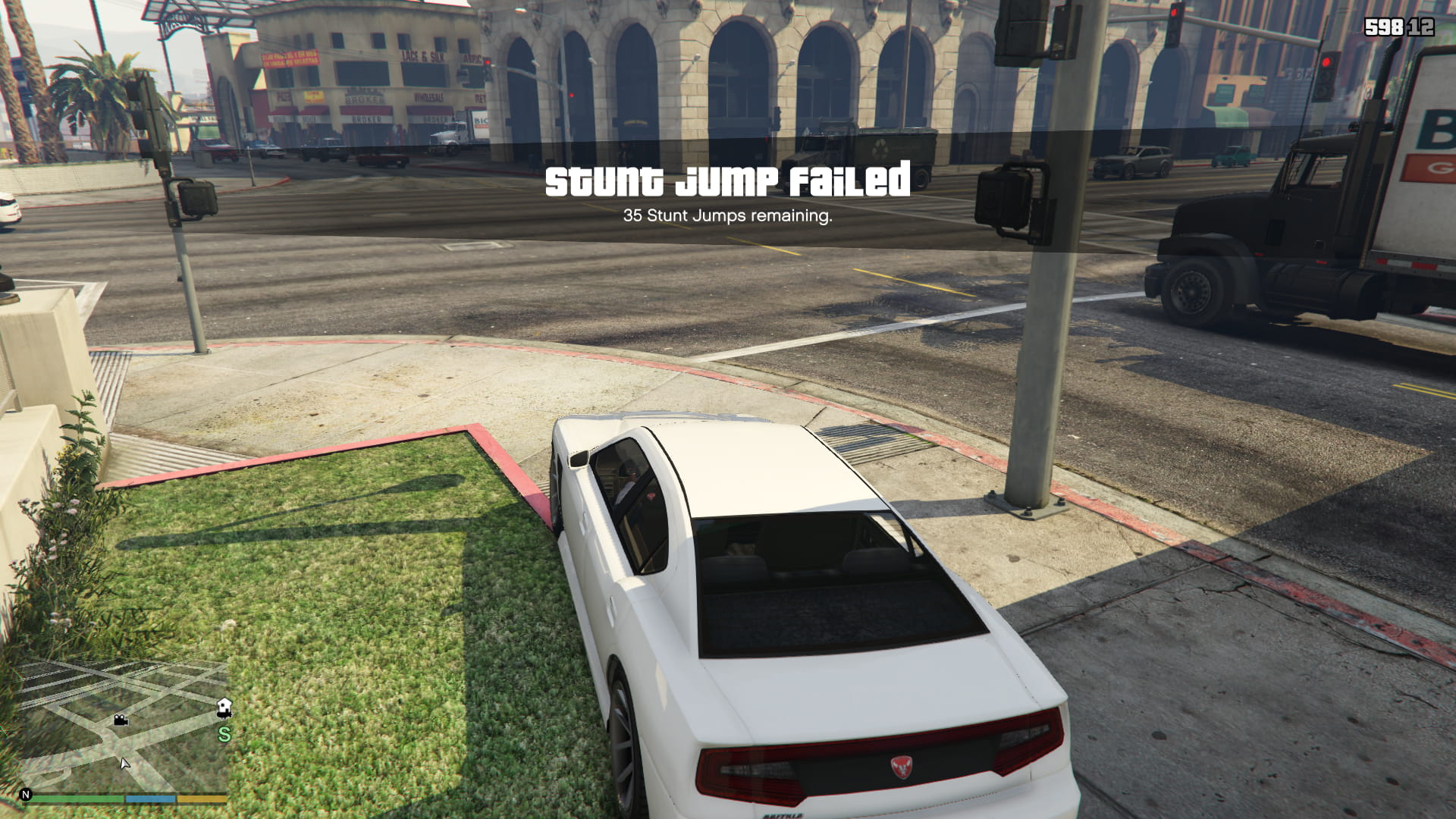
Angled Regions

Okay, but we don't know how angled stunt jumps work! To test, we'll use the airport jump, since it's defined by an angled jump, but runners have already done the majority of the work in setting approximate bounds for where we can land. The code to add the airport jump is:

ADD_STUNT_JUMP_ANGLED(
  -963.171387, -2778.506104, 14.478280, // start{X,Y,Z}1
  -965.736084, -2777.121094, 19.463949, // start{X,Y,Z}2
  -8.000000, // radius1

  -988.829712, -2830.789062, 11.964780, // end{X,Y,Z}1
  -1027.989014, -2895.436035, 16.958050, // end{X,Y,Z}2
  -18.000000, // radius2

  -967.195984, -2811.716064, 14.552100, // cam{X,Y,Z}
  150, 0, 0 // unk{1,2,3}
);

(This is where the demonstration video for the teleportation mod was recorded!)

Conjecture: Axis-aligned cuboid, rotated by angle

This is the first potential solution that I thought of: Let's say that an 'angled' region is just a plain axis-aligned region, but before we do any calculations, we rotate the entire world's yaw around the rectangle's centre-point by the given extra float value.⁵

Then, we 'rotate the world' to do calculations with the 'angled' rectangle:

This means that the detection code is also extremely simple, we just rotate the target point around the rectangle's centre point by the given angle:

function isInsideRotatedRect(
  point: Vector2,
  minCorner: Vector2,
  maxCorner: Vector2,
  angle: number
): boolean {
  const centrePoint = (minCorner + maxCorner) / 2;

  point -= centrePoint;
  point = point.rotate(angle);
  point += centrePoint;

  return point;
}

So, let's test it! The values for the airport jump are:

• startUnk: -8.0
• endUnk: -18.0

We'll assume these are degrees, since it wouldn't make sense to have these integer values as radians.

To calculate the points for the rotated rectangle, we'll write a quick-and-dirty little Python program:

from math import pi, sin, cos

# Simple axis-aligned rectangle constructor, yielding four points:
def aa_rectangle(min_corner, max_corner):
  min_x, min_y = min_corner
  max_x, max_y = max_corner

  return (min_corner, (min_x, max_y), max_corner, (max_x, min_y))


def rotate_rectangle(rect, angle):
  # The central point for the rectangle is the average of all coordinates:
  centre_point = (0, 0)
  for point_x, point_y in rect:
    centre_point = (centre_point[0] + point_x, centre_point[1] + point_y)
  centre_point = (centre_point[0] / 4, centre_point[1] / 4)

  new_rect = [None] * 4

  for i, point in enumerate(rect):
    point_x, point_y = point

    # Since rotation is super simple when rotating about the origin,
    # we just translate the rectangle, do our rotation, and translate back.

    point_x -= centre_point[0]
    point_y -= centre_point[1]

    theta = (pi / 180) * angle
    point_x = point_x * cos(theta) - point_y * sin(theta)
    point_y = point_y * cos(theta) + point_x * sin(theta)

    point_x += centre_point[0]
    point_y += centre_point[1]

    new_rect[i] = (point_x, point_y)

  return new_rect

if __name__ == "__main__":
  corners = [float(v) for v in input("Corners: ").split()]
  assert len(corners) == 4

  min_x = min(corners[0], corners[2])
  min_y = min(corners[1], corners[3])

  max_x = max(corners[0], corners[2])
  max_y = max(corners[1], corners[3])

  rect = aa_rectangle((min_x, min_y), (max_x, max_y))

  angle = float(input("Angle: "))
  rect = rotate_rectangle(rect, angle) # heh.

  print(rect)

$ python3 calculate-rotated-rect.py
Corners: -988.829712 -2830.789062 -1027.989014 -2895.436035
Angle: -18
[(-1037.0192243162842, -2885.013077611761), (-1017.0422110243856, -2829.703389285405), (-979.7995016837158, -2841.212019388239), (-999.7765149756142, -2896.521707714595)]

We can use this program to calculate a rotated point for the airport jump, and it... doesn't work, even with a lot of leeway to put us very far 'inside' where the rectangle would be.

Conjecture: Locus of a Line

Okay, since the FiveM native database describes the two unknown values as 'radii', perhaps we take the two points in space, draw a line between them, and allow the car to land anywhere within the given radius of the line. This means that the car, upon landing, must be within a certain capsule.

Let me show you what I mean in 2D: First, we take a line segment l between two position vectors, start and end.

Then, we only accept points in space that lie within a certain distance, d, of the line:

Recall that the endRadius for the airport jump is -18⁶, so we can just use that for our value of r.

This actually works for most cases! But unfortunately, it doesn't check out when we do something like:

const testPoint = end + (end - start).normalize() + 0.5;

where we follow the line but 'go past' the end point by a small amount.

I'm actually pretty glad; remember that the goal is to visualize where the jump regions are. Rendering this racecourse-looking locus is a bit less trivial than a rotated box.

Conjecture: A rectangle constructed from a line and a width

I was imagining doing the 'Locus of a line' model above, but chopping off the two hemispheres at either end, since that's where the experimental tests seemed to be failing. But that's just making a rectangle! So, we construct a rectangle by taking the line segment between two points, and using a perpendicular width that perpendicularly extrudes the line into a rectangle.

We create a perpendicular line segment of length w that bisects l:

And create a rotated rectangle bounded by the two line segments. We also define a middle point m, which lies at the centre of one of the rectangle's extruded sides. This is useful to know when we're rendering the regions, but it's not required for calculating whether a point is contained.

The algorithm to determine if a point lies within this rectangle is actually pretty simple: We just find the closest point on the line segment l and check if we are within w distance of that point. However, if the closest point on the line segment is at either of the line's extremes, we know that the point cannot be 'next to' the line segment, and therefore is not in the rectangle bounded by the line.

function isPointWithinAngledRect(
  point: Vector2,
  start: Vector2,
  end: Vector2,
  width: number
): boolean {
  const delta = end - start;
  const distanceSq = delta.x * delta.x + delta.y * delta.y;

  /*
   * In this Stack Exchange Math post, https://math.stackexchange.com/a/2193733:
   * We create a value 't' and write l as start + t * delta, meaning that we lerp
   * between the start and the end by t. When t is 0, the value is the same
   * as start; and at 1, the value is the same as end.
   *
   * Then, we can construct a function to get the vector from the input point and
   * an interpolated point on the line:
   * f(t) = (1 - t) * start + t * delta - point
   * Then, we turn that into a minimization problem and Do Algebra™ to get
   * the magic formula for the value of 't':
   */
  const t = -(delta.dot(start - point) / distanceSq);

  // If t lies on (or beyond!) either extreme of the line,
  // we can immediately return false:
  if (t >= 1 || t <= 0) return false;

  // Otherwise, the distance between the closest point and the test point
  // must be less than half the rectangle's width:
  const pointToLineVec = start + t * delta - point;
  const distanceToLineSq =
    pointToLineVec.x * pointToLineVec.x + pointToLineVec.y * pointToLineVec.y;

  // (width / 2)² is (width² / 4)
  return distanceToLineSq < (width * width) / 4;
}

And all the experiments I tried checked out, so I'm fairly certain this is exactly how Rockstar are doing the stunt jump calculation.

Here's a threshold value at the airport:

Conclusion

If you want to work with Rockstar's angled regions system, there are only a few things you need to know.

First up, an angled region looks like this:

struct AngledRegion {
  struct Vector3 startPoint;
  struct Vector3 endPoint;
  float width;
}

function AngledRegion.contains(point: Vector3): boolean {
  // Throw out any values which do not lie, vertically, between the corners:
  const minZ = min(this.startPoint.z, this.endPoint.z);
  const maxZ = max(this.startPoint.z, this.endPoint.z)
  if (point.z < minZ || point.z > maxZ)
    return false;

  const deltaX = endPoint.x - startPoint.x;
  const deltaY = endPoint.y - startPoint.y;

  // Squared length of hypotenuse:
  const sqH = (x, y) => x * x + y * y;

  const t = sqH(
    delta.x + (startPoint.x - point.x),
    delta.y + (startPoint.y - point.y)
  ) / sqH(deltaX, deltaY);

  // Throw out any values that aren't 'next to' the line
  if (t >= 1 || t <= 0)
    return false;

  // Interpolate by t from start to end:
  const pointOnLineX = start.x + t * deltaX;
  const pointOnLineY = start.y + t * deltaY;

  // The distance from the target point to the point on the line
  // must be less than (width / 2):
  return sqH(pointOnLineX - point.x, pointOnLineY - point.y) < (width * width) / 4;
}

This opened up the opportunity to create a mod for GTA V that shows the locations of the stunt jumps, which has actually been featured in all the demonstrative media in this post.

Happy jumping! ⁷